The Distribution Used to Describe the Behaviour of Rare Events

Rare Events the Sample Decision and Conclusion Establishing the type of distribution sample size and known or unknown standard deviation can help you figure out how to go about a hypothesis test. No rule of thumb but Any disease is considered a rare event.

Poisson Distribution

Poisson Distribution is a distribution function used to describe the occurrence of rare events or to describe the sampling distribution of isolated counts.

. We only need to use the mean and standard deviation to explain the entire. Hypergeometric Distribution eg the number of de-fective items in the sample when a sample of. A normal distribution is determined by two parameters the mean and the variance.

A basis for prediction b. This is the distribution that is used to construct tables of the normal distribution. A standard normal distribution SND.

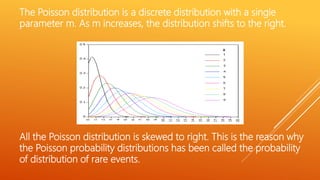
Discrete random variables take a countable number of integer values and cannot take decimal values. Earthquakes in the past million years not so rare. The distribution used to describe the behaviour of rare eventsis the Poisson Distribution.

B use the normal curve if the observed frequency distribution consists of many observations. D use the normal curve if the observed frequency distribution is reasonably compact. ThePoisson Distributionis a statistical probability related formula that describes the rate of the behaviour of rare events.

The binomial distribution for example evaluates the probability of an event occurring several times over a given number of trials and. The hypergeometric distribution is similar to the binomial distribution in that both describe the number of times a particular event occurs in a fixed number of trials. The first distribution is unimodal it has one mode roughly at 10 around which the observations are concentrated.

An explanation of why the events are related c. Earthquakes in the past ten years rare. The distribution could involve popularities random numbers of occurrences of events with various probabilities etc.

An indication that an underlying third factor is at work. More about Guassian distribution and how it can be used to describe the data and observations from a machine learning model. The second distribution is bimodal it has two modes roughly at 10 and 20 around which the observations are concentrated.

In this post well focus on understanding. Uniform Discrete Distribution eg the number of dots facing up if a balanced die is tossed. Knowing that two events are correlated provides a.

Add Solution to Cart. Number of events in an interval of time or area when the events are occurring at a constant rate. The Poisson distribution is used to describe the distribution of rare events in a large population.

The Poisson distribution is a discrete probability distribution that describes the probability of the number of events discrete random variable from a random process in a fixed interval. This is the most studied distribution and there is an entire sub-field of statistics dedicated to Gaussian data. The rare event of interest is an extreme deliberate act of violence destruction or socioeconomic disruption such as an attack of 911 scale or greater.

Our rule of thumb. The mean mode and median of the distribution are equal. More typically the Poisson is used to approximate the binomial for situations when p is small but n is large enough for the approximation to be reasonable rather than the binomial being used to approximate the Poisson.

It is not a realistic goal to anticipate and prevent all rare events but it may be possible to make. Depends on time unit. With large n Poisson probabilities are easier to calculate.

However there are several other factors you should consider when working out a hypothesis test. The normal distribution is simple to explain. A set of real numbers a set of vectors a set of arbitrary non-numerical values etc.

A normal distribution with a mean of 0 and a standard deviation of 1 is called a standard normal distribution. A probability distribution is a mathematical description of the probabilities of events subsets of the sample space. Shape is similar to BinomialPoisson distribution.

Number of items in a batch of random size. Proof that as one increases the other also increases d. Discrete random variables are usually counts.

Binomial Distribution eg the number of cured pa-tients among all the patients who use the drug in a study involving testing the e ectiveness of a new drug. The solution discusses binomial distribution used to model the number of rare events. Linear Regression with Rare Events Linear Regression with Rare Events Rare event.

This means that the likelihood of an event is proportional to the size of the area of opportunity and that the rate of occurrence for the rare events is constant throughout the area of opportunity Next given that the counts are Poisson the times between events will be modeled by an exponential distribution. C use the normal curve if there arent any minor irregularities in the observed frequency distribution. Any event as frequent as a disease can be considered rare.

The difference is that binomial distribution trials are independent whereas hyper-geometric distribution trials change the probability for each subsequent trial and. Mutation acquisition is a rare event. The term is often used loosely with no definition or arbitrary definition but precise definitions are possible.

Design reliability tests where the failure rate is considered to be constant as a function of usage. The sample space often denoted by is the set of all possible outcomes of a random phenomenon being observed. For example at any particular time there is a certain probability that a particular cell within a large population of cells will acquire a mutation.

Show activity on this post. It may be any set. The third distribution is kind of flat or uniform.

The Behavioral Turn In Flood Risk Management Its Assumptions And Potential Implications Kuhlicke 2020 Wires Water Wiley Online Library

Poisson Distribution An Overview Sciencedirect Topics

Poisson Distribution